简述了计算机信息的储存方式、十六进制表示法，布尔代数和C语言中的位运算、逻辑运算和移位操作三类运算符。

2.1 信息储存

​ 大多数计算机使用8位的块，或者字节(byte)，作为最小的可寻址的内存单位，而不是访问内存中单独的位。机器级的程序将内存视为一个非常大的字节数组，称为虚拟内存(virtual memory)。内存的每个字节都由一个唯一的数字来标识，称为它的地址(address)，所有可能的地址的集合就称为虚拟地址空间(virtual address space)。虚拟地址空间只是一个展现给机器级程序的概念性映像，实际的实现是将动态随机访问存储器(DRAM)、闪存、磁盘存储器、特殊硬件和操作系统软件结合起来，为程序提供一个看上去统一的字节数组。

十六进制表示法

​ 一个字节有8位组成。在二进制表示法中，它的值域是$00000000_2\sim 11111111_2$。如果看成十进制整数，它的值域就是$0_{10}\sim255_{10}$。两种符合表示法对于表述位模式都不是很方便所以引入了十六进制(hexadecimal)表示法。用十六进制书写，一个字节的值域为$00_{16}\sim FF_{16}$。

​ 在C语言中，以 0x或 0X开头的数字常量为被认为是十六进制的值。

字数据的大小

​ 每台计算机都有一个字长(word size)，指明指针数据的标称大小(nominal size)。因为，虚拟地址是以这样的一个字节来编码的，所以字长决定的最重要的系统参数就是虚拟地址空间的最大大小。也就是说，对于一个字长为 $w$位对的机器而言，虚拟地址的范围为$0$~$2^w-1$，程序最多访问$2^w$个字节。

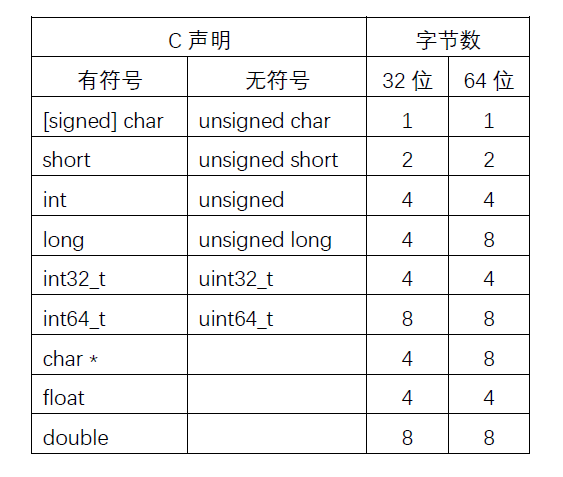
寻址和字节顺序

​ 对于跨越多字节的程序对象，我们必须建立两个原则：这个对象的地址是什么，以及在内存中如何排列这些字节。在几乎所有的机器上，多字节对象都被存储为连续的字节序列，对象的地址为所使用字节中最小的地址。

​ 排列表示一个对象的字节有两个通用的规则。考虑一个$w$位的整数，其位表示为$[x_{w-1},x_{w-2},···，x_1,x_0]$，其中$x_{w-1}$是最高有效位，而$x_0$是最低有效位。假设$w$是8的倍数，这些为就能被分组成为字节，其中最高有效字节包含位$[x_{w-1},x_{w-2},···,x_{w-8}]$，而最低有效字节包含位$[x_7,x_6,x_5,x_4,x_3,x_2,x_1,x_0]$，其他字节包含中间的位。某些机器选择在内存中按照从最低有效字节的顺序储存。前一种规则——最低有效字节在最前面的方式，称为小端法(little endian)。后一种规则——最高有效字节在最前面的方式，称为大端法(big endian)。

​ 假设变量 x的类型为 int，位于地址 0x100处，它的十六进制值为 0x01234567。地址范围0x100~0x103的字节顺序依赖于机器的类型：

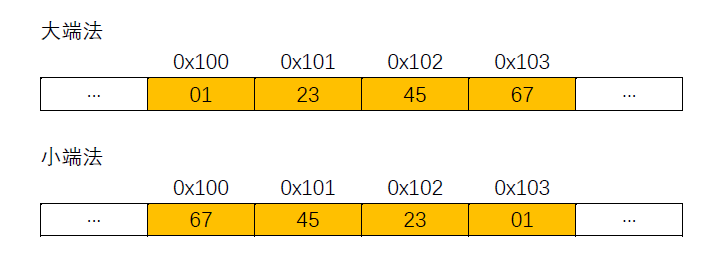
​ 对于大多数应用程序员来说，其机器所使用的的字节顺序是完全不可见的。无论为哪种类型的机器所编译的程序都会得到同样的结果。不过有时候，字节顺序会成为问题。首先是在不同类型的机器之间通过网络传送二进制数据是，一个常见的问题是当小端法机器及其产生的数据被发送到大端法机器（或者反过来），接受程序会发现，字里的字节成了反序的，为了避免这类问题，网络应用程序的代码编写必须遵守已建立的关于字节顺序的规则，以确保发送方机器将它的内部表示转换为网络标准，而接收方则将网络标准转换为它的内部表示。

第二种情况是，当阅读表示证书数据的字节序列是字节顺序也很重要。

第三种情况是，当编写规避正常的类型的程序时，字节顺序很重要。在C语言中，可以通过强制类型转换(cast)或联合(union)来允许以一种数据类型引用对象，而这种数据类型与创建这个对象是定义的数据类型不同。大多数应用编程都强烈不推荐这种编码技巧，但是他们对系统级编程来说是非常有用，甚至是必需的。

表示字符串

​ C语言中字符串被编码为一个以null（其值为0）字符结尾的字符数组。每个字符都由某个标准编码来表示，最常见的是ASCII字符吗。字符串在使用ASCII码作为字符码的任何系统上都将得到相同的结果，与字节顺序和字大小规则无关。因而，文本数据比二进制数据具有更强的平台独立性。

表示代码

​ 不同的及其类型使用不同的且不兼容的指令和编码方式。即使是完全一样的进程，运行在不同的操作系统上也会有不同的编码规则，因此二进制代码是不兼容的。二进制代码很少能在不同机器和操作系统组合之间移植。

​ 计算机系统的一个基本概念就是，从机器的角度来看，程序仅仅只是字节序列。机器没有关于原始程序的任何信息，除了可能有些用来帮助调试的辅助表以外。

布尔代数简介

​ 二进制是计算机编码、存储和操作信息的核心，所以围绕数值0和1的研究已经演化出了丰富的数学知识体系。

​ 最简单的布尔代数实在二元集合${0,1}$基础上的定义，布尔运算 $\sim$ 对应于逻辑运算 NOT，在命题逻辑中用符号 $\neg$ 表示。也就是说，$P$ 不为真时，$\neg P$ 为真，反之亦然。 相应地， 当 $P$ 等于0时，$\sim P$ 等于 1，反之亦然。布尔运算 $\&$ 对应于逻辑运算 AND， 在命题逻辑中用符号 $\wedge$ 表示。当 $P$ 和 $Q$ 都为真时，我们说 $P\wedge Q$ 为真。相应的，只有当 $p=1$ 且 $q=1$ 时，$p\& q$ 才等于1。布尔运算 $|$ 对应与逻辑运算 OR， 在命题逻辑中用符号 $\vee$ 表示。 当 $P$ 或者 $Q$ 为真时，我们说 $ P\vee Q$ 成立。相应地，当 $p=1$ 或者 $q=1$ 时，$p| q$ 等于1。布尔运算 $\hat{}$ 对应逻辑运算异或，在命题逻辑中用符号 $\oplus$ 表示。 当 $P$ 或者 $Q$ 为真但不同时为真时，我们说 $ P\oplus Q$ 成立。当 $p=1$ 且 $q=0$，或者 $p=0$ 且 $q=1$， $p\hat{} q$ 等于1。

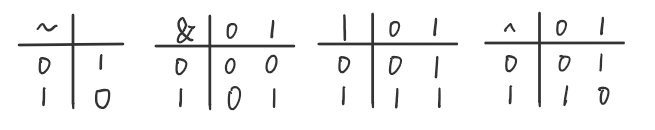
我们可以将上述4个布尔运算扩展到位向量的运算，位向量就是固定长度为$w$、由0和1组成的串。位向量的运算可以定义成参数的每个对应元素之间的运算。假设 $a$ 和 $b$ 分别表示位向量 $[a_{w-1},a_{w-2},···,a_0]$ 和 $[b_{w-1},b_{w-2},···,b_0]$。 我们将 $a\&b$ 也定义为一个长度为 $w$ 的位向量，其中第 $i$ 个元素等于 $a_i\& b_i$，$0\leqslant i < w$。可以用类似的方式将运算 $|$ 、$\hat{}$ 和 $\sim$ 拓展到位运算上。

位向量是一个很有用的应有就是表示有限集合。我们可以用位向量 $[a_{w-1},a_{w-2},···,a_0]$ 编码任何子集 $A\subseteq {0,1,···,w-1 }$，其中 $a_i = 1$ 当且仅当 $i\in{A}$。

C语言中的位级运算

​ C语言的布尔运算符号：| OR（或），& AND（与），~ NOT（取反），^ EXCLUSIVE-OR（异或）。

C语言中的逻辑运算

​ C语言的逻辑运算符号||、&&、!，分别对应命题逻辑中的OR、AND 和 NOT。

C语言中的移位操作

​ C语言提供了一组移位运算符<<、>>，向左或者向右移位模式。对于左移x << k来说，x 向左移动 $k$ 位，并在右端补 $k$ 个 0。对于右移x >> k来说，机器支持两种形式的右移：逻辑右移和算术右移。逻辑右移就是在左端补 $k$ 个 0。算术右移是在左端补 $k$ 个最高有效位的值。