Dijkstra 算法是一个最短路径算法，常用于解决非负有权图中的最短路径问题。本文通过示例介绍了 Dijkstra 算法，并给出了 C++ 的算法实现和一种优化策略。

Dijkstra 算法

介绍

Dijkstra 算法通过保留目前为止所找到的每个顶点 $v\in V$从 $s$ 到 $v$ 的最短路径来工作的。初始时，起点 $s$ 的路径权重被赋为 $0\ (dis[s]=0)$，同时把其他路径的长度设为无穷大。当算法结束后，$dis[v]$ 存储的便是从 $s$ 到 $v$ 的最短路径，如果路径不存在，则 $dis[v] = \infty $。

松弛操作是 $Dijkstra$ 算法的基础操作：如果存在一条从 $u$ 到 $v$ 的边，那么从 $s$ 到 $v$ 的一条新路径就是将边 $w(u,v) \in E$ 添加到从 $s$ 到 $u$ 的路径尾部，拓展出一条从 $s$ 到 $u$ 的路径。这条新路径的长度是 $dis[u] + w(u,v)$。如果这个值比已知的 $dis[v]$ 小，那么可以替换原先的 $dis[v]$，并将 $path[v]$ 的值更改为 $u$。松弛操作已知运行到所有的 $d[v]$ 都代表 $s$ 到 $v$ 的最短路径的长度值。

示例

直接看介绍可能还不理解，我们可以看如下的图

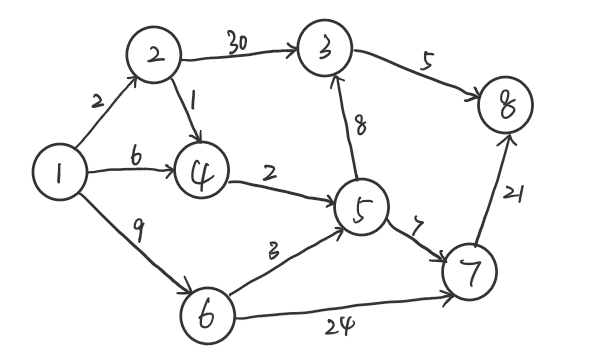
假设起点 $s = 1$，我们将 $s$ 压入路径 $q$ 中， $vis[s] = 1(true)$ , $dis[s] = 0$，寻找路径中最近的点 $u$ 即 $u=1$ ，将 $u$ 扔出路径，此时 $u$ 点连通 $v = 2,4,6$ 三点，将 $\{2,4,6\}$ 压入路径 $q$ 中，计算 $w = w(u,v)+dis[u]$，根据 $dis[v] = min(dis[v],w)$ 更新 $dis$ ,此时$dis=\{0,2,\infty,6,\infty,9,\infty,\infty,\infty\}$ ,若 $dis[v]$ 更新，就使 $path[v] = w$ ，此时 $path = \{1,1,0,1,0,1,0,0\}$ 。

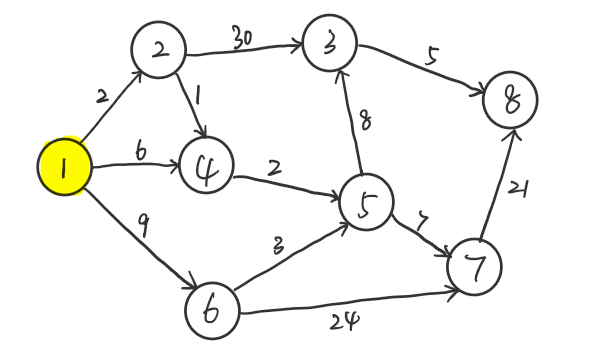
第二次，我们查找路径中与起点 $s$ 距离最近的点$u$ ，此时 $u=2$，同样将 $u$ 扔出路径并将 $vis[u]=1$， 因为$u$ 点连通 $v = 3,4$ 且 $vis[v] = 0 (false)$，所以更新路径 $q=\{3,4,6\}$，更新 $dis=\{0,2,32,3,\infty,9,\infty,\infty\} $，更新$path=\{1,1,2,2,0,1,0,0\}$。

同理，$u=4$，$vis[u]=1$，$q=\{3,5,6\}$，$dis=\{0,2,32,3,5,9,\infty,\infty\}$，$path=\{1,1,2,2,4,1,0,0\}$。

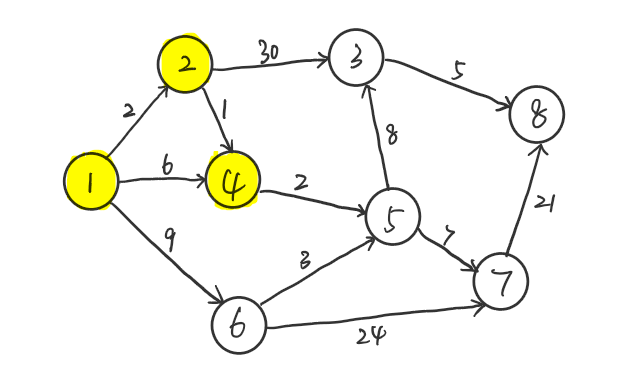
同理，$u=5$，$vis[u]=1$，$q=\{3,6,7\}$，$dis=\{0,2,13,3,5,9,12,\infty\}$，$path=\{1,1,5,2,4,1,5,0\}$。

同理，$u=6$，$vis[u]=1$，$q=\{3,7\}$，$dis=\{0,2,13,3,5,9,12,\infty\}$，$path=\{1,1,5,2,4,1,5,0\}$。

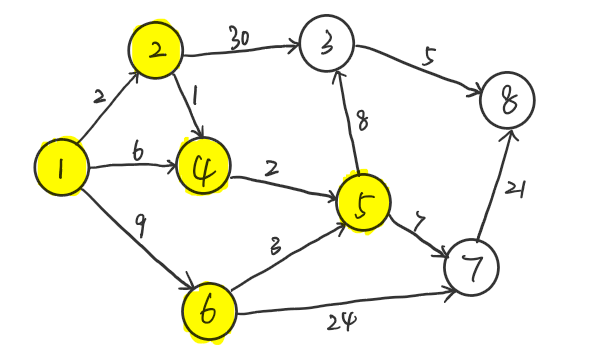
同理，$u=7$，$vis[u]=1$，$q=\{3,8\}$，$dis=\{0,2,13,3,5,9,12,33\}$，$path=\{1,1,5,2,4,1,5,7\}$。

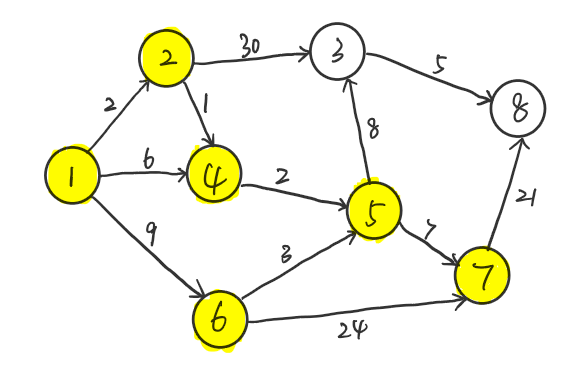
同理，$u=3$，$vis[u]=1$，$q=\{8\}$，$dis=\{0,2,13,3,7,9,12,28\}$，$path=\{1,1,5,2,4,1,5,3\}$。

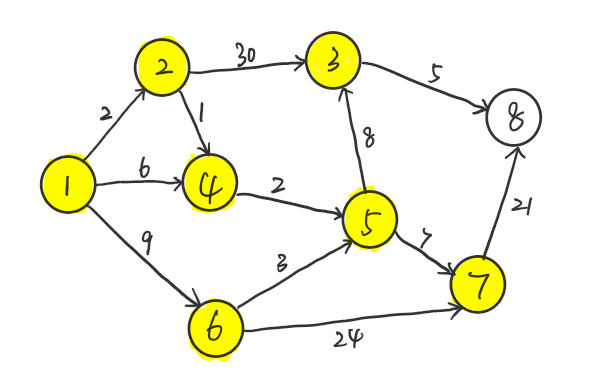
最后$u=5$，$vis[u]=1$，$q=\{\}$ 为空，到此 $Dijkstra$ 算法顺利完成！

实现及优化

首先定义 $dis,vis,path,node$。

int dis[N];
bool vis[N];
int path[N];

stuct node
{
    int u, v, w;
    node(int _u, int _v, int _w):u(_u), v(_v), w(_w){}
    bool operator<(const node& n) const
    {
        return v > n.v;
    }
};

初始化 $dis,vis,path$

void init()
{
    for (int i = 1; i <= n; i++)
    {
        dis[N] = INT_MAX;
    }
    memset(vis,0,sizeof(vis));
    memset(path,0,sizeof(path));
}

因为有删除操作，为了减少复杂度，选择了用 std::list<> 来存储路径。

void dijkstra(vector<vector<node>>& vec, int s)
{
    list<int> q;
    init();
    q.push_back(s);
    dis[s] = 0;
    path[s] = s;
    while (!q.empty())
    {
        auto k = q.begin();
        for (auto it = q.begin(); it != q.end(); it++)
        {
            if (dis[*it] < dis[*k])
                k = it;
        }
        int v = *k;
        q.erase(k);
        vis[v] = true;
        for (auto& i : vec[v])
        {
            if (!vis[i.v] && i.w + dis[v] < dis[i.v])
            {
                dis[i.v] = i.w + dis[v];
                path[i.v] = v;
                if(find(q.begin(),q.end(),i.v)==q.end())
                    q.push_back(i.v);
            }
        }
    }
}

因为在每次寻找离起点最近的点都要花费 $O(V)$ 的复杂度，所以考虑把点都存在堆中，在 C++ 中一般使用std::priority_queue<>优先队列，将每条边以 $\{u,v,w(u,v)+dis[u]\}$ 的形式压入队列中，队列顶端的元素即为边通向的顶点到起点距离的最小值，此时只要花费 $O(log(E))$ 的复杂度。总体的复杂度从 $O(V^2+E)$ 变为了 $O((E+V)log(E))$，当图为稀疏图时，使用堆的算法效率明显更高。

void dijkstra(vector<vector<node>>& vec, int s)
{
    init();
    priority_queue<node> q;
    q.push(node(s,s,0));
    while (!q.empty())
    {
        node k = q.top();
        q.pop();
        if(vis[k.v]) continue;
        vis[k.v] = true;
        dis[k.v] = k.w;
        path[k.v] = k.u;
        for(auto& i : vec[k.v])
        {
            q.push(node(i.u, i.v, i.w + dis[i.u]));
        }
    }
}