并查集是一种树型的数据结构，主要用于处理一些不交集的合并及查询问题。本文通过样例介绍了并查集，并给出了 C++ 算法的实现和两种优化方案。

并查集

在计算机科学中，并查集是一种树型的数据结构，主要用于处理一些不交集（Disjoint Sets）的合并及查询问题。有一个联合-查找算法（Union-find Algorithm）定义了两个用于此数据结构的操作：

• Find：确定元素属于哪一个子集。它用来确定两个元素是否属于同一子集。
• Union：将两个子集合并成同一个几何。

为了更加精确的定义这些方法，需要定义如何表示集合。一种常用的策略是为每个集合选定一个固定的元素，称为代表，以表示整个集合。接着，Find(x) 返回 x 所属集合的代表，而 Union 使用两个集合的代表作为参数。

并查集介绍和实现

市场上原来有 $1,2,3,4,5,6$ 这六家公司，各自经营着自己的生意。

有一天，$4$ 找到了 $1$ 说，最近形式不大好，要不我们两家公司合并成一家，$4$ 觉得自己的名字不够气派，就跟着 $1$ 叫同一个名字了。

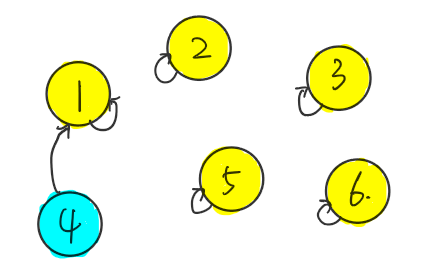
过了不久，$2$ 也想着找人合作，就找到了 $4$，$4$ 说我已经改叫 $1$ 了，你跟我和合作就是跟 $1$ 合作，$2$ 和 $1$ 商量了一下，$2$ 也觉得自己的名字不好听，也改成 $1$ 的名字了。

$3,6$ 一看市场形势，也开始和 $5$ 商量起了合并的事宜，他们决定最后名字就是 $5$ 了。

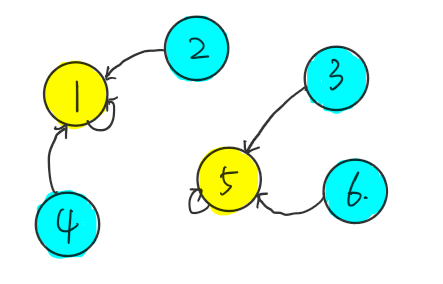
可是 $5$ 合并的太晚了， 已经临近破产，$2$ 公司看到机会跟 $6$ 公司商量事宜，其实最后就是 $1$ 和 $5$ （他们合并后的公司）商量，结果 $5$ 很无奈，被合并了，最后所有公司归为 $1$ 管理了。

其实这个合并的图是一个树状结构，寻找每个集合的代表元素，只要层层向上访问父节点搜索即可，直到到达树的根节点。根节点的父节点是它自身。我们可以直接把这幅图表示成一棵树。

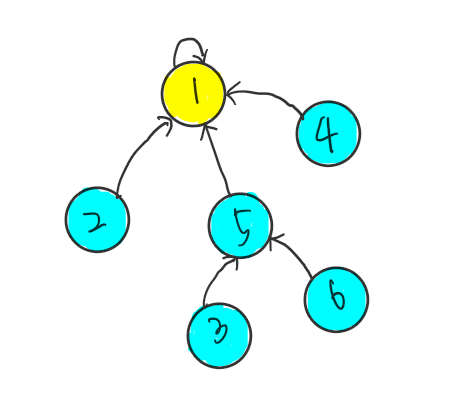
代码实现

根据上面例子的步骤，我们可以轻松写出简单版本的并查集代码。

初始化

int root[N];
void init(int n)
{
    for (int i = 1; i <= n; i++)
        root[i] = i;
}

我们用 root 数组存储每个节点的父节点， 刚开始，先把所有节点的父节点初始化为自己。

查询

int find(int x)
{
    if (root[x] == x)
        return x;
    else
        return find(root[x]);
}

查询这个节点的根节点时，我们使用递归的思想：一层一层访问该节点的父节点，直到访问到根节点（即父节点是自身）。

合并

void merge(int i, int j)
{
    root[find(i)] = find(j);
}

合并两个节点也很节点，只要把其中一个的根节点的父节点设置为另一个的父节点即可。

优化并查集

前面说的简单的并查集其实效率比较低。

路径压缩

我们可以看以下场景：

我们进行 merge(2,3) 和 merge(2,4) 操作后，图变为如下：

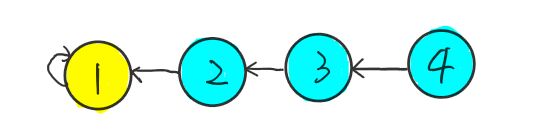
这是一条长链，随着节点的不断增多，这条链会越来越长，我们从链最底部找到其根节点的消耗也越来越多。

如果图是这样的，我们就不必层层查询根节点了。

那么怎么实现呢？我们可以使用路径压缩的方法，在每次寻找元素根节点的时候，把它的父节点直接设为根节点，这样在下一次查询后，只要一次就能找到根节点了。

同样用递归的方式，把沿途的父节点全设置为根节点：

int find(int x)
{
    if (x != root[x])
    {
        root[x] = find(root[x]);
    }
    return root[x];
}

按秩合并

由于路径压缩只对访问过的路径进行压缩，不是每个节点的父节点都是根节点。所以并查集的结构仍然可能是负载的。看下面的情形：

$8$ 要和 $7$ 合并，这是我们有两种方案，$7$ 作为 $8$ 的父节点和 $8$ 作为 $7$ 的父节点这两种方式：

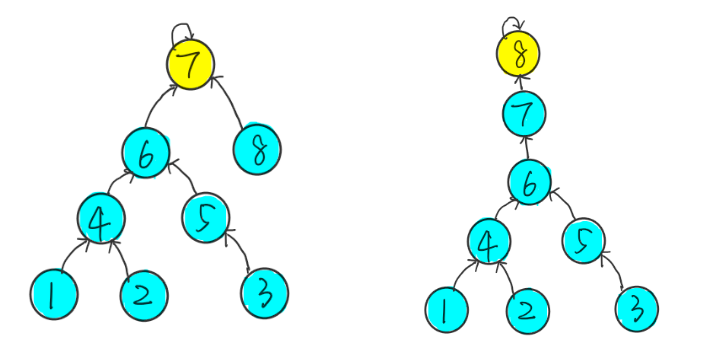
显然第一种方式效率更加高。

因为如果把 $8$ 作为 $7$ 的父节点，会使得数的深度（树中最长链的长度）加深，原来树的每个节点到根的距离都变长了，后面我们每次查询根节点复杂度也会变高。而把 $7$ 作为 $8$ 的父节点就不会有这个问题。因此我们每次合并的时候都应该把简单的树合并到复杂的树上面，保证每次合并到根节点距离变长的节点数量最少。

运用这个思想我们可以写出相关的代码。

初始化

我们用 rank 数组来表示每个根节点对应的树的深度。一开始将所有的 rank 置为 1。

int rank[N];
void init(int n)
{
    for (int i = 1; i <= n; i++)
    {
        root[i] = i;
        rank[i] = 1;
    }
}

合并

合并时比较两个根节点的 rank 值，将 rank 小的向 rank 大的树合并。如果两个树深度相同，则合并后新树的 rank 值需要加一。

void merge(int i, int j)
{
    int x = find(i), y = find(j);
    if (rank[x] <= rank[y])
        root[x] = y;
   	else
        root[y] = x;
   	if (rank[x] == rank[y] && x != y)
        rank[y]++;
}

注意路径压缩和按秩合并一起使用时，可能会破坏按秩合并的准确性。